회귀 분석에는 제약식을 포함할 수 있습니다. 제약이 없다면 측정하려는 가중치 W가 기하급수적으로 커질 수 있으며 이로 인해 분산이 커지는 문제가 발생하게 됩니다.
이를 해결하기 위해 여러가지 제약식을 사용할 수 있습니다.
1. 라쏘 회귀(Lasso Regression) - L1 Regularization
라쏘 회귀는 L1 Loss 형태인 |θ|를 제약식으로 추가하여 특성값의 가중치가 극히 낮은 값이면 0으로 수렴하게 하여 특성을 제거하는 방법입니다. 특성을 0으로 만든다는 것은 상대적으로 bias를 증가시켜 오버피팅을 방지할 수 있습니다.
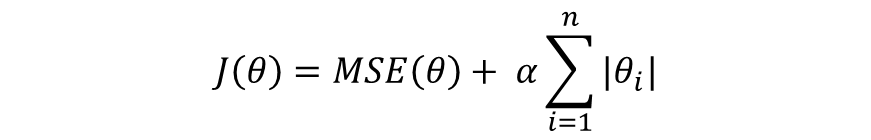
2. 릿지 회귀(Ridge Regression) - L2 Regularization
릿지 회귀는 L2 Loss 형태인 θ^2를 제약식으로 추가하여 모델 예측에 영향을 거의 미치지 않는 특성에 0에 가까운 가중치를 주는 방법입니다.

3. 엘라스틱넷(ElasticNet)
엘라스틱넷은 라쏘 회귀와 릿지 회귀의 최적화 지점이 서로 다르기 때문에 두 제약식(정규화)항을 합쳐서 가중치 r로 제약 정도를 조절하는 방법입니다.

결국 위 세 가지 가중치 제약 회귀 방법은 회귀 가중치의 값이 커져서 오버피팅을 방지하기 위한 방법이라고 볼 수 있습니다. (가중치 값이 커지는 것을 제한)
정리하면 특성의 수가 많고 그 중 일부분만 중요한 특성이라면 라쏘를,
특성의 중요도가 전체적으로 비슷하다면 릿지가 좀 더 좋은 모델을 만들기에 좋습니다.
또한 데이터의 수가 많고 라쏘와 릿지를 모두 반영하고 싶다면 엘라스틱넷을 사용할 수 있습니다.
사이킷런의 Lasso, Ridge, ElasticNet 클래스를 사용해 보겠습니다.
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression, Lasso, Ridge, ElasticNet
from sklearn.metrics import mean_squared_error
raw_boston = datasets.load_boston()
X = raw_boston.data
y = raw_boston.target
# X.shape, y.shape: (506, 13) (506,)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=1)
# X_train.shape, X_test.shape, y_train.shape, y_test.shape: (379, 13) (127, 13) (379,) (127,)
std_scaler = StandardScaler()
X_train = std_scaler.fit_transform(X_train)
X_test = std_scaler.transform(X_test)
lasso = Lasso()
ridge = Ridge()
elastic_net = ElasticNet()
lasso.fit(X_train, y_train)
ridge.fit(X_train, y_train)
elastic_net.fit(X_train, y_train)
print(lasso.coef_)
# [-0. 0. -0. 0. -0. 1.98095526
# -0. -0. -0. -0. -1.35346816 0.
# -3.88203158]
print(lasso.intercept_)
# 22.344591029023764
print(ridge.coef_)
# [-1.05933451 1.31050717 0.23022789 0.66955241 -2.45607567 1.99086611
# 0.18119169 -3.09919804 2.56480813 -1.71116799 -2.12002592 0.56264409
# -4.00942448]
print(ridge.intercept_)
# 22.344591029023768
print(elastic_net.coef_)
# [-0.41185619 0.12517736 -0.242448 0.35325324 -0.43649162 1.96540308
# -0.02116576 -0. -0. -0.16013619 -1.2626002 0.32546709
# -2.36558977]
print(elastic_net.intercept_)
# 22.34459102902376
pred_lasso = lasso.predict(X_test)
pred_ridge = ridge.predict(X_test)
pred_elastic_net = elastic_net.predict(X_test)
lasso_mse = mean_squared_error(y_test, pred_lasso)
# 32.74719740278476
ridge_mse = mean_squared_error(y_test, pred_ridge)
# 21.894849212618745
elastic_net_mse = mean_squared_error(y_test, pred_elastic_net)
# 35.196183733607924coef_를 통한 lasso의 회귀 계수(가중치)를 보면 0인 값이 보입니다.
이와 다르게 ridge의 회귀 계수에는 0이 없습니다.
또한 elastic_net의 회귀 계수에는 0인 값이 있긴 하지만 lasso보다는 그 수가 적습니다.
'AI > Machine Learning' 카테고리의 다른 글
| [Machine Learning] 나이브 베이즈 (Naive Bayes) (0) | 2023.05.24 |
|---|---|
| [Machine Learning] 로지스틱 회귀 (Logistic Regression) (1) | 2022.09.29 |
| [Machine Learning] 선형 회귀 (Linear Regression) (0) | 2022.09.28 |
| [Machine Learning] K-최근접 이웃 알고리즘 (KNN) (0) | 2022.09.28 |
| [Machine Learning] 모델 성능 평가 - 분류, 회귀 (0) | 2022.09.27 |